Notes On Math Connections
General topics:
- Cartesian coordinates
- Transformational geometry
- translation--Cartesian distance, ratios between distances
- rotation--angle measures
- dilation--ratio and percentage
- reflection--Cartesian axes
Structured Inquiries:

1) Each plait (y shape) in the braid is scaled down by 90% of the previous plait.
- If the first is 1 inch wide, how wide is the second? (answer: 0.9 inches).
- How wide is the third? (answer: 0.81 inches)
- How wide is the nth plait? (answer: 0.9n)
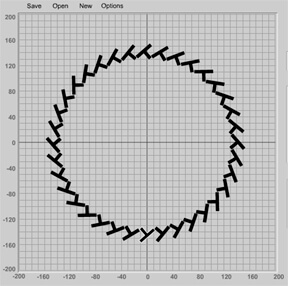
2) We can also look for some specific shapes to explore: circles and spirals are probably the best examples. Geometry of the circle, for instance, can be explored by looking at the relations between rotation and iteration. A circular braid will be generated any time you have a braid with rotation and sufficient numbers of plaits (that is, sufficiently high number of iterations). So you can ask students to do an inquiry exercise:
How many plaits are required to create a complete circle? It depends on the rotation--the higher the rotation, the fewer plaits you need. If you are only rotating by 1 degree in each plait, then you will need 360 plaits to go full circle (thats only 359 iterations, because you get one plait to start with; in other words there is a zeroth iteration at start). A 10 degree rotation will require only 36 plaits to make a full circle. And so on. Having them discover this relationship on their own would be an empowering exercise. Do these results change if you dont use the default translation of 100%? If you dont use the default of 100% dilation? [TIP:use a small starting dilation, like 20%, so that they can fit all of the braid on the screen at once]
3) Another good exercise concerns relations between braids. As you transition from one braid to the next, which parameters change? Below is a model in which students can first apply an empirical, inductive approach, estimating the starting angle for each braid. They can then approach the same problem analytically: there are 12 braids from zero to 90 degrees, 90/12 = 7.5. So the starting angle for each braid is 7.5 degrees greater than the one before it.

