Royal Style: 45 degrees

There are also purely abstract designs that make use of multiples of 45 degrees, as we see in this textile. Modern Mangbetu report that the creation of a design reflected the artisan's desire to "make it beautiful and show the intelligence of the creator" (Schildkrout and Keim p. 100). This suggests another reason for artisans to adhere to angles that are multiples of 45 degrees: if there were no rules to follow, then it would have been difficult to compare designs and demonstrate one’s ingenuity. By restricting the permissible angles to a small set, they were better able to display their geometric accomplishments.

Combining this 45 degree angle construction technique with the scaling properties of the ivory carving from Figure 6 can reveal its underlying structure. The carving has three interesting geometric features. First, each head is larger than the one below it, and faces in the opposite direction. Second, each head is framed by two lines, one formed by the jaw and one formed by the hair; these lines intersect at approximately 90 degrees. Third, there is an asymmetry: the left-side shows a distinct angle about 20 degrees from the vertical.

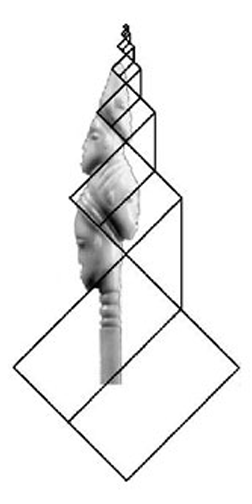
All of these features can be accounted for by the structure shown here. This sequence of shrinking squares can be constructed by an iterative process, bisecting one square to create the length of the side for the next square, as indicated in the diagram. We will never know for certain if this iterative squares construction was the concept underlying the sculpture’s design, but it does match the features identified above. In the ivory sculpture, the left side is about 20 degrees from the vertical. In the iterative squares structure, the left side is about 18 degrees from the vertical. Here we see that the construction algorithm can be continued indefinitely, and the resulting structure can be applied to a wide variety of math teaching applications, from simple procedural construction to trigonometry.