When braiders create cornrow patterns, they use four geometric concepts: translation, rotation, reflection, and dilation. This tutorial will explain how these geometric concepts are used by braiders, and show how they can be applied to create simulations of cornrow hairstyles in this software.

Each cornrow braid is made up of a series of y-shaped twists or "plaits".

Above the image of the real braid, you can see a simulated braid. How many plaits do you guess are in the simulated braid? Write down your guess in your notebook and then click on the braid for the answer. Then continue to the next lesson.

Our computer simuation starts with one original plait. Each time we add a plait, it is called an "iteration." Play with the iteration number in this simulation to get as close as you can to this braid. Write down your answer in your notebook and continue to the next lesson, Dialation.

In this simulation, each plait is the same size. Sometimes, we want the plaits to dilate, either grow larger or smaller in each iteration. Let's figure out how dilation works.

Question: Let's say the original plait is 1 in wide. And let's make this iteration 50% of the size of the original. How wide is the first iteration plait?

Now you can see how iteration works: you dilate the current plait to make the next plait. By dilating each time, you make increasingly smaller copies. The changes accumulate-pretty soon we have timy plaits.

Play with the dilation value in this simulation to get as close as you can to this braid. Write down your answer in your notebook and then continue to the next lesson.

In this simulation pictured on this page, each plait has the same orientation. But we want the plaits to rotate in each iteration. Let's figure out how rotation works.

Question: Let's say we ritate the plaits 15 degrees in each iteration. The original plait is not rotated at all, so we will call that 0 degrees. The first iteration is rotated 15 degrees, and the third 30 degrees. How many degrees is the plait rotated in the third iteration?

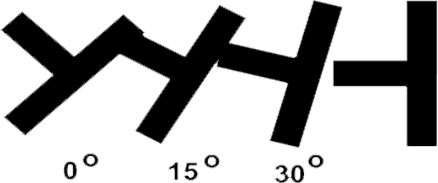
Again, you can see how iteration lets you accumulate changes: every time you make a new plait, it gets rotated in addition to the last plait's rotation.

Now try experimenting with the amount of rotation in the simultion above. When you think you have the right answer, enter it in your notebook. What happens if you use a negative rotation? Write down your answer in your notebook and then continue to the next lesson.

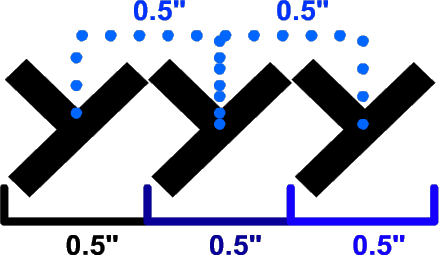
Hairstylists have fine control over the distance between each plait: tight braids have the plaits very close together, while loose braids have them farther apart. In this simulation, the distance between each plait is greater than we want it to be. Let's figure out how to tighten the braids by controllign the amount each plait is moved (translated) in each iteration.

Example: Let's say the original plait is 0.5 inches wide. For each iteration, the plait will be translated 100% of the width of the original plait. The first iteration will translate 0.5 inches.

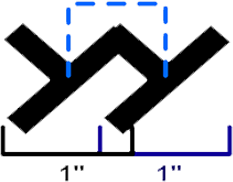
Question: Let's say the original plait is 1 inch wide. And let's make this first iteration translate 75% of the width of the original. How far away is the plait in the first iteration?

How does the software keep track of all four geometric transformations? Below, you can see a plait with an arrow called a vector. Vectors are used in physics to show that something has a position, a direction, and a quanity (like speed or force). In our case, the quantity is the plait size. Plait vector tells you:

1. The center of rotation. Note that the plait rotates around the blue vector anchor at the visual center of the plait.
2. The direction of translation. Note that each time the plait is rotated, the vector rotates with it. Rotations are relative to the vector in each iteration. So the rotations "accumulate" with each iteration, giving an overall curve to the braid.
3. The width of the plait copy. Note that as each plait is dilated, the vector is dilated with it. So the dilation is relative to the vector, and it will accumulate with each iteration.
4. The location of the axis of reflection. Note that both X axis and Y axis reflections pass through the vector anchor.

Congrats! You completed the tutorial. You can either: