Password:
Origins
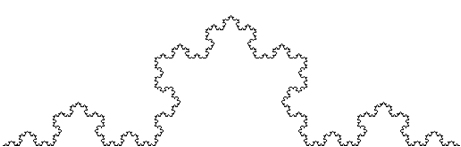
Fractals have the property of self-similarity: a small part looks like the whole. We can see that in this image of a Koch curve, a fractal named for Swedish mathematician Helge von Koch. At top we see three big clusters, like the arms and head of a lumpy snowman. But each is made of similar clusters, and so on down to infinity. How did Koch construct such an infinitely wiggly curve?
Scaling

The Koch curve begins as the simple seed shape seen here, just 4 lines. Then we shrink down the seed shape--as we say in mathematics we apply a scaling transformation --and replace its first line with a miniature version of itself. We do that for all 4 lines, and now we have the output of the first iteration.
Recursion

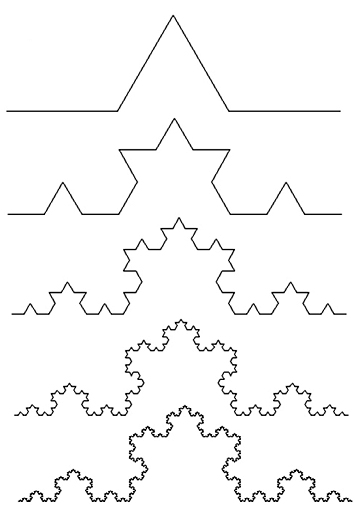
Iteration 1, 2, 3, 4, and 5.
In each iteration we do the same process, replacing lines with miniature versions of the original seed, and then bringing the output in as the input for the next iteration. We refer to a process in which outputs are used as inputs as a "recursive loop."
Koch Curve
Click "Edit Mode" to enter the edit mode. Click and hold on a node and drag it to move it around, or single click to move it around then click again to place it. Double click on a line between nodes to insert a new node. It will be the color you have selected. To change colors, click on a color at the bottom then click on the line you wish to change. When you are done creating your seed shape, click on "Iterate Mode" and move from "Iter 1" on up to eight to see the fractal take shape!
Red: Regular
Blue: Flip
Orange: Invert
Purple: Invert and Flip
Green: Passive Line
Gray: Invisible
Delete/Backspace Key: Delete Node
Recursive Loops

In Africa, recursive loops are sometimes represented as a snake that bites its own tail. Just as contemporary computer science uses recursion to model the fractal structures in nature, Indigenous African knowledge recognizes and makes use of the "self-generating" properties of certain natural and social systems.
Another snake symbol in Africa represents well-being that lasts forever. They say that the snake is infinitely long, but it can fit in a finite space, because it has "coiled back on itself." As we will see, fitting infinite length into a finite space is also a good description of a fractal.
Measuring Fractals
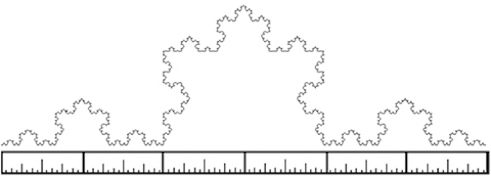
| When the ruler size is: | Koch Curve | The measured length is: |
|---|---|---|
| 6 inches |
|
6 inches |
| 2 inches |
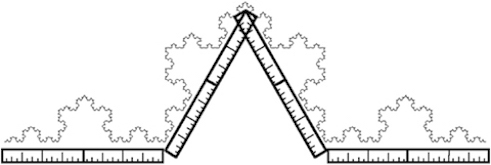
|
8 inches |
| 0.5 inches |
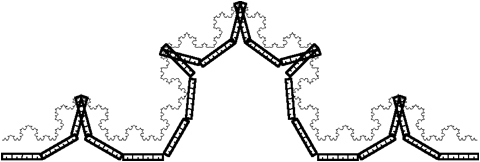
|
12 inches |
The smaller we make the ruler, the more we measure. The "real" length is infinity! But how can we distinguish the "high" Koch curves from the "low" Koch curves if they all measure infinity?
Fractal Dimension
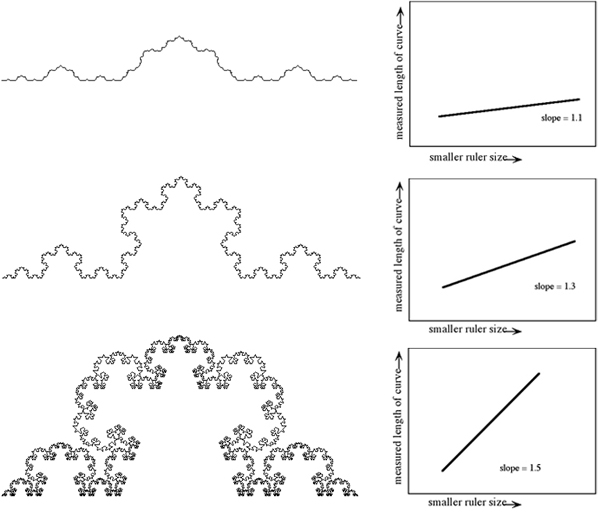
As we shrink down the ruler size, the length increases to infinity. But how fast does it increase? For a smooth Koch curve, it increases slowly. For a rough one it increases quickly. The slope of the line tells you how fast or slow. It is the fractal dimension.
A line has one dimension, a square 2, But fractals are in-between, so they have a fractional dimension! That is how they can fit infinity into a finite space. Their curve is so torturous that it is more than one dimensional. In fact it can get so wiggly that it actually does become a space-filling curve, in which case the fractal dimension will be 2.0 (a surface!).
Base Line
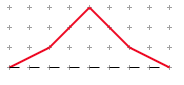
segment 1

segment 2
In each iteration we replaced each line with a scaled-down seed shape. The amount it scales by is the scaling ratio. It is the ratio between the length of the line to be replaced, and the length of a baseline. The dashed line is the baseline. So the scaling ratio of the first segment is about 2.2/8, the length of the line segment, over the length of the baseline.