Fractals in Science

Fractals can model many aspects of nature, from cosmology to molecules. The fractal aspects of Romanesco broccoli are pretty easy to spot, but other natural objects take a little practice to see their scaling patterns. In this section, you can practice by experimenting with simulations of natural objects. You will also learn how fractals can be applied to the design of objects in the artificial world of technology.

A coil of rope is a linear spiral. It has the same distance between each revolution. But nature produces logarithmic spirals, which increase the distance between each revolution. This simple scaling pattern permits organisms to grow while retaining a similar shape. Try changing the spiral's form by editing the seed shape. The stem is a passive green line, and the "growing tip" is a self-replicating red line. This is common in living things: a growing edge leaves behind dead cells (such as a tree's outer bark) or minerals (such as a snail's shell), providing a strong, protective structure.

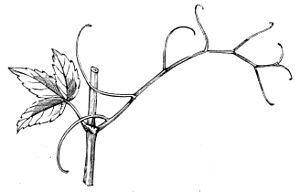
Here we see an example from a kiwi vine: the older woody stem is passive, and the young red shoot is active. When it grows old enough, it will be the passive source of a new vine in the next "iteration". The spiral fern above does this as a continuous gradient, so its a little easier to see the process in discrete stems.

Baobab tree

The frequent droughts of the African bush require that trees must be able to store water and reduce evaporation. The baobab stores water in its fat trunk (up to 26,000 gallons). To reduce evaporation, it keeps its surface area small by quickly scaling down branches. In our simulation this means the self-replicating or "active" line is small in comparison to the passive lines. What happens if you adjust that? How might evolution take advantage of that system?

What is the evolutionary advantage of fractals? They combine a maximum of surface area with a maximum of flow, so trees take in more light, lungs exchange more oxygen, kidneys filter more waste, neurons connect with more neurons. Plants in the desert need to conserve water, so they tend to have a lower fractal dimension (a cactus has less surface area per volume than a fern). And DNA itself is a recursive loop, so it may be that fractals naturally arise from mutation.

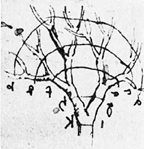
Sketch from Da Vinci's notebook showing his analysis of branching.

In 1510, Leonardo Da Vinci wrote: "All the branches of a tree at every stage of its height when put together are equal in thickness to the trunk." Thus, if a "mother" branch produces two "daughter" branches, the area of a cross-section of the mother is equal to the sum of the areas of the cross-sections of the daughters. This means that the ratio of the daughter-diameter to the mother-diameter will be about 0.707 -- can you show why? Can you find the ratio for mother branch length to daughter branch length?

In botany, the growing tip is called an "apical meristem." Press "edit" and you will see two red lines representing the apical meristems. Click off "snap to grid" and then change the size and angle of the red lines by dragging their endpoints.

Click the "Seed" drop-down menu under "Edit Mode" to select "Davinci Tree 3" or "Davinci Tree 4" for trees with higher branch numbers.

Spleenwart fern

The fern appears to be a very complicated shape, but looking at the seed in this simulation (click on "Edit Mode") you can see it is only 4 lines! Knowing what we just learned from the baobab tree, see if you can create ferns for both wet and dry environments. Note that your trial and error experiments are just like those of nature "trying out" mutations.

Dendritic Ice Crystal

River Basin

Spirals in Turbulence

Sierpinski Carpet Antenna

Sierpinski Triangle Antenna

Antenna using Koch curve

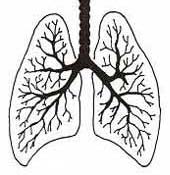
Human lungs

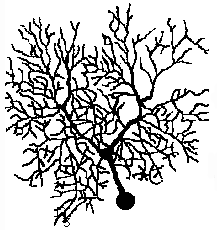
Guinea pig Purkinje cell (neuron)

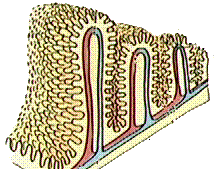
Intestinal villi