Summer
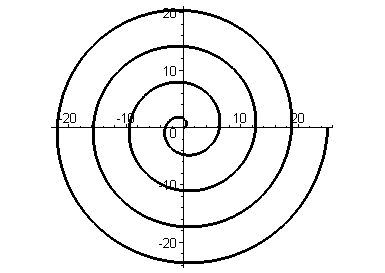
We can model the twisting vertical reeds in the camus basket as a three-dimensional spiral. Spiral symmetry is an important concept in many Native American knowledge systems. A two-dimensional spiral can be modeled in polar coordinates: Here we set the distance from the center, radius r, equal to the angle (theta) of the radius: r = theta. As the angle sweeps around the plot, the radius moves farther from the center.
A Shoshone camus root gathering basket (ISU museum). Note the beautiful twist of the vertical willow reeds.
Polar coordinates
Spiral Symmetry
The "Sun Dagger" is a spiral petroglyph by which the Chacoans (previously known as "Anasazi") were able to read the seasons using a shaft of sunlight falling between two stone slabs; the spiral center marked the position of the sun at the summer solstice. For photo and details click here:
http://www.lapahie.com/Chaco_Sun_Dagger.cfm (Harrison Lapahie Jr.)
The Polar Coordinate System
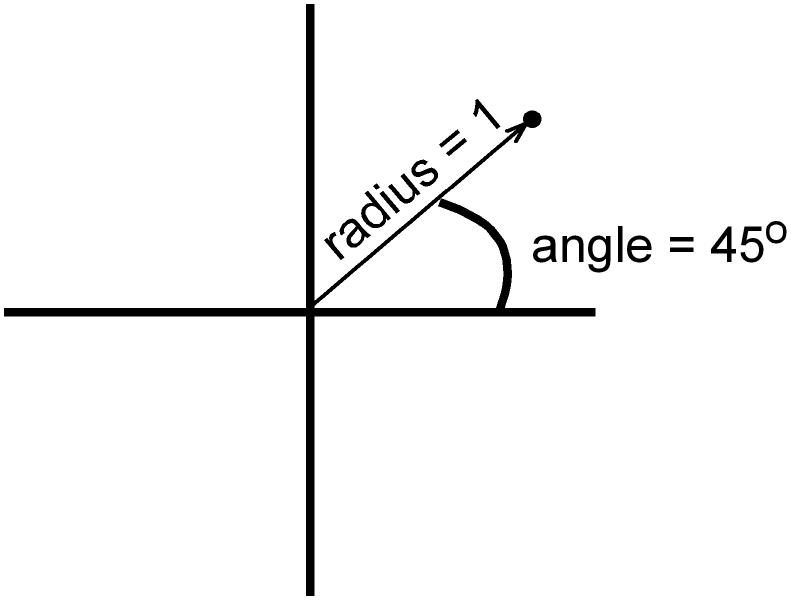
You are probably familar with the cartesian coordinate system, where points are specified by their place along horizontal and vertical axes, represented by X,Y. The polar coordinate system specifies points by the distance from the center (called the radius ("r")), and an angle from the horizontal (usually called theta). Here we see the point 1,45.
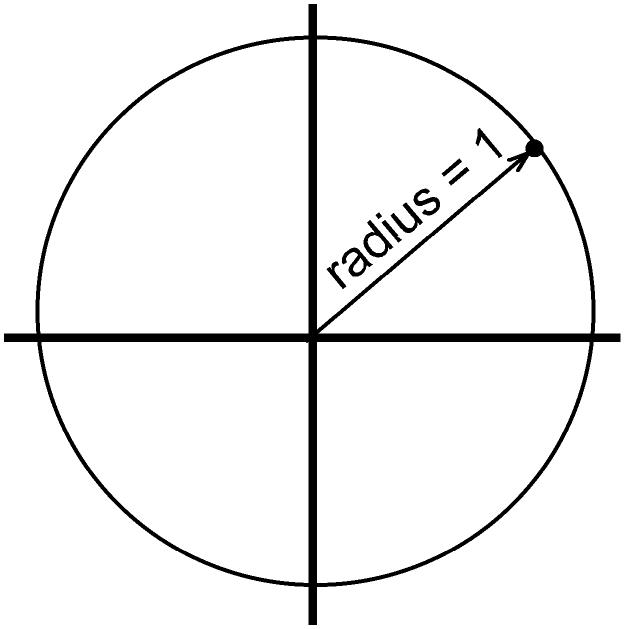
It is very easy to draw a circle with polar coordinates: we just say r=1 for theta = 0 to 360. If you wanted only a quater of a circle, you could say r=1 for theta = 0 to 90.
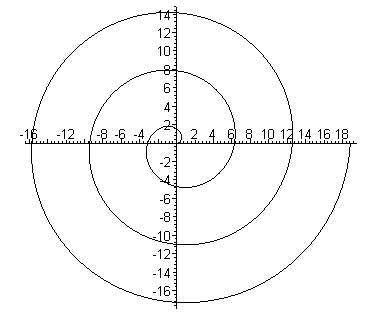
It is also easy to draw a spiral with polar coordinates: you can just make r increase as you go around the circle. For example, you can say r=theta. Now every time theta gets bigger, r gets bigger.
Since r is a length, it makes sense to think of theta as how far you have gone around a circle -- a quarter revolution, a half revolution, etc. We can see that this spiral was generated by 3 revolutions.
Rather than call it revolutions, mathematicians use the measure "radians," which is a multiple of the number Pi (3.14159...). One full revolution is 2Pi radians. Since this spiral was made by the equation r=theta, and we had 3 revolutions, the radius at the end of the is 3*2Pi=18.8.
Helix
Now to make a three-dimensional spiral, or "helix." Here are some examples turning along a length measured in radians. Which one is closest to the helix we see in the basket above?
Imagine the vertical length is time, and the turns are turns of the seasons. What would the events in your life look like if you plotted them along a helix?
8 turns in 8Pi radians
2 turns in 8Pi radians
1 turn in 8Pi radians
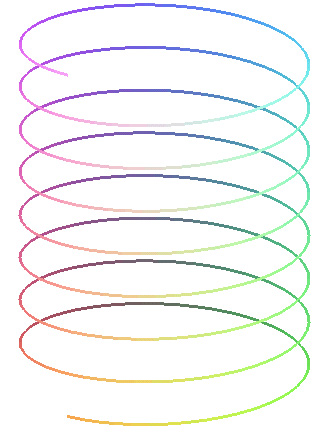
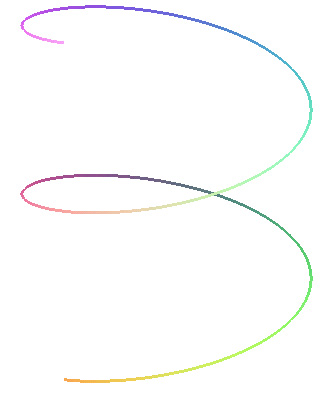
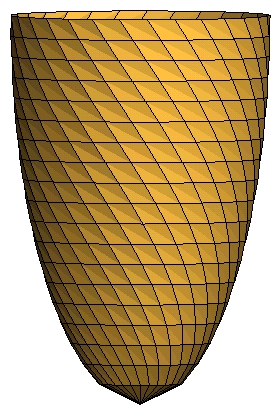
Now we can try our hand at simulating the basket. Go to the simulation window and experiment with the following parameters: depth, width, twist, lines across width (n), lines across length (m).
The twist factor is the number of turns along the length of the basket.