Winter

A Shoshone pine nut winnowing basket (photo from ISU museum). Its shape is specifically designed for the winnowing motion.

Shoshoni pine nut winnowing basket in use. (photos from ISU museum) Why not make this a circular rim, as we see in the camus basket?
1) The rose petal shape allows a more firm area (pointed end) in which the upward force of the toss can be transferred to the nuts, but the downward force of the nuts can be absorbed by the less firm area to prevent the nuts from bouncing out.
2) Due to entropy, the nuts coming down will be covering a larger area than the nuts tossed upward, so a broader catch area is required.


We can think of the rim of the winnowing basket as a rose-petal shape, pointed at one end and broad at the other. The wild rose is an important plant in Shoshone culture. The wild rose was traditionally an important source of vitamin C in the Shoshoni diet in the form of rose hips. It appears in Shoshoni arts in two different forms: side view and top view. The side view of the rose, shown at left in beadwork by Candy Titus, provides a more concrete image.
The top view of the rose is more abstract, and is represented by five-fold symmetry, as shown in the decorated bag from the tribal museum.
It is worth noting that the more abstract, geometric designs are actually older, previous to contact with Europeans. We usually hear how Native American culture was more concrete, and European culture more abstract and mathematical, but in this case the reverse is true.
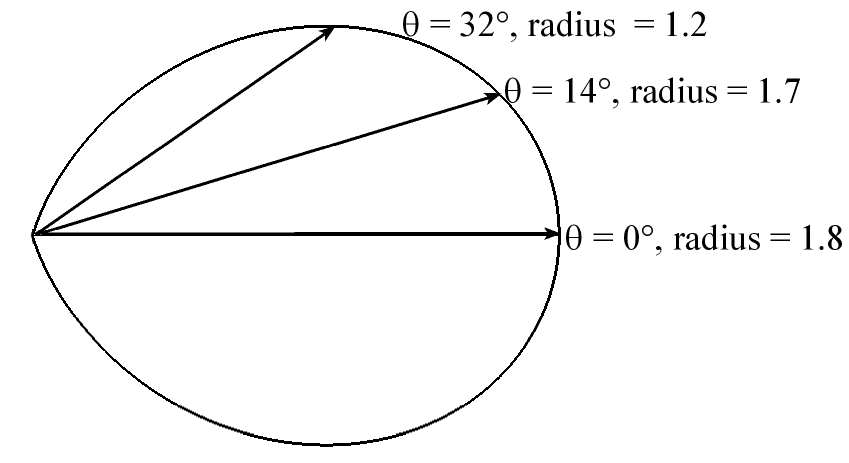
A common way to make such petal shapes in mathematics is by graphing in polar coordinates. The polar coordinate system is very similar to the Shoshone basket-making technique. Note that mesh inside the basket originates from the many struts attached to the pointed end of the petal. In the same way, the polar coordinate system always has the radius attached to the origin point.
Here is a polar graph of the function radius = cos(2*theta)+0.8. Shoshone basket makers have to figure out how long each strut would be for each angle theta, just as the function tells you the radius for each theta value.
The basket depth is created by having strut length longer than the radius across the plane of the basket rim.
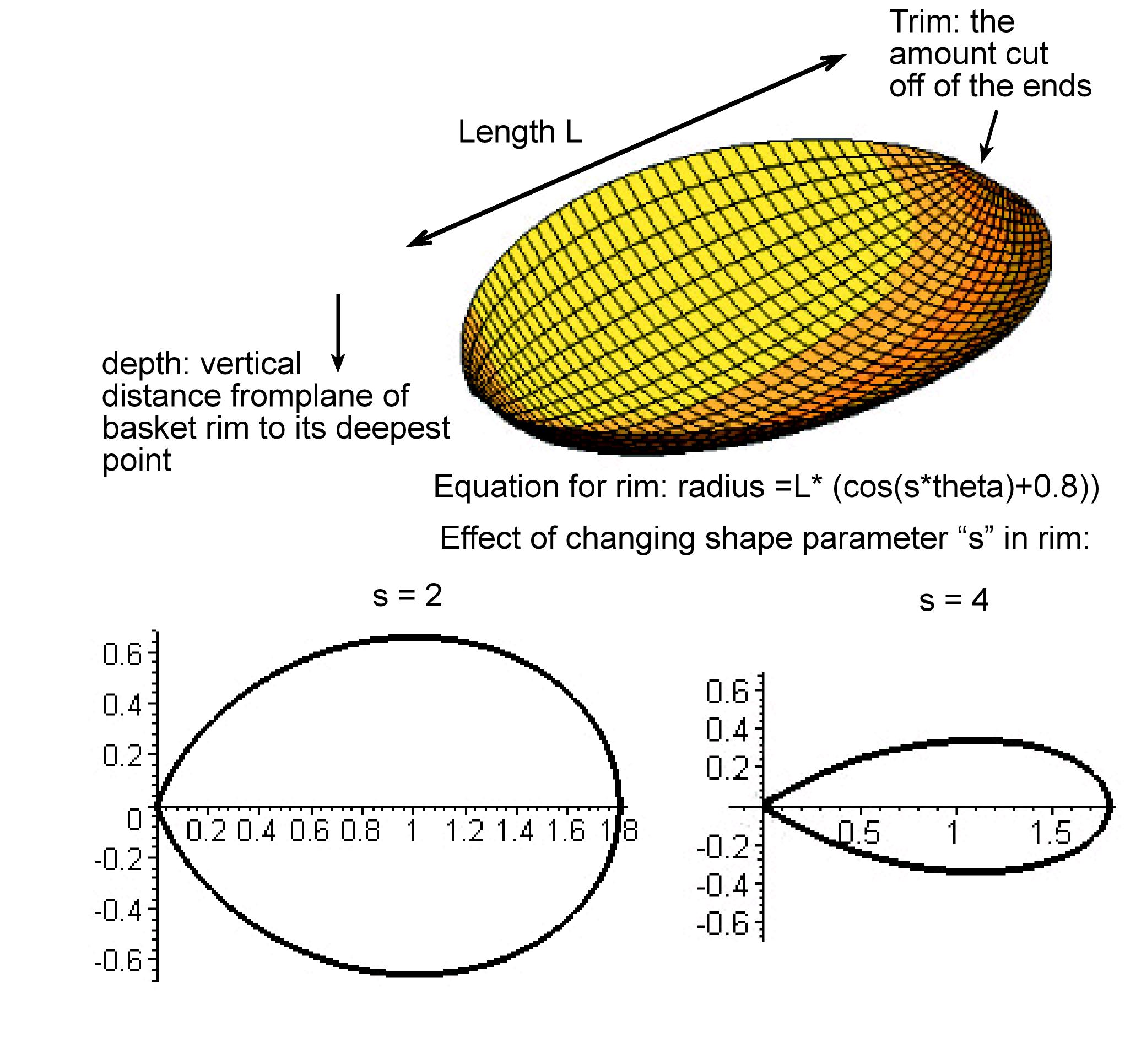
Now lets make a winnowing basket! Go to the simulation window and experiment with the following parameters:
length =_____
depth =_____
shape: s =_____
trim = _____
number of lines across width: n =____
number of across length: m =____
Use the mouse to change a value, then hit "enter" (you may have to do that more than once, check to see if the cursor is changed to an hourglass, if so just wait).
Try to see how close you can get the simulation to look like the original.
Try to create a totally new shape of your own design.
To save the image, left-click on it and "copy."
Then paste into our collection. Don't forget to type your name underneath.