Back to Adinkra Spirals
Why Do We See Logarithmic Spirals in Biological Structures?
Cell Growth
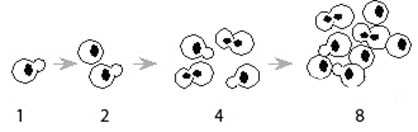
The simple idea of one cell splitting into two cells can help us understand log scaling. Each "daughter" cell splits into two more the next month, and so on. If we plot the sum of cells (S) each time period (t), we notice that it follows the curve S = 2t. You can see a simulation here. The equation is S = P(1+I)t where P is the principle (starting) number of cells, and I is the increase rate (the rate of cell reproduction). S = P(1+I)t = 1*(1+1)t = 2t.
Of course real cells don't all reproduce at the same time. Suppose only half reproduced each month (rate of reproduction 0.5), then the graph is less steep: S = 1.5t Its the same equation for a bank account: P is the Principle amount of dollars, just like the principle number of cells you start with. Interest rate I = 0.5, just like the cell reproduction rate. Compounded each month t, then total savings S= P(1+I)t = 1(1+0.5)t = 1.5t.
The image at bottom is a nautilus shell, split in half so you can see how the mollusk developed a new chamber as it grew. You can experiment with a simulation here. Each chamber in the simulation is 104% larger than the previous. If the size is proportional to the number of cells, that means the cells reproduce on average at a rate of 0.04.
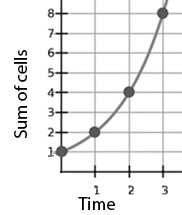
Cell Growth Graph
In addition to growing by 104%, each chamber in the simulation is rotated 18 degrees from the previous. If you increase the growth rate-- say, 105%-- you will see that the spiral creates gaps--more like a horn than a shell. So if you increase the growth rate, you have to make the shell more "tightly coiled" to prevent gaps. The West African artisans who create Adinkra stamp carvings describe the growth rate of spirals in similar ways-- the terms they use in Twi, "aboapua awan" and "ntitim awan," translate into English as "tightly coiled" and "loosely coiled". Which is a better match to the nautilus shell?

Nautilus

Tightly coiled
("aboapua awan")

Loosely coiled
("ntitim awan")
Scaling Constant
If you said "tightly coiled" is a better match, you were right! Our eyes have put us on the right track; now lets see if numbers can help us make that more exact. The spiral’s equation in polar coordinates is radius = eC*theta, where e is the base of the natural log, theta is the angle, and C is a constant. You can think of C as the “coil” parameter. For a tightly coiled log spiral like the one above, C is smaller: in this case 0.2. For a loosely coiled spiral like the one below, C is larger (0.4). In the simulation here you can explore the cultural curves of adinkra and biological curves of nature, using the blocks you see below the spirals.




We can also measure spirals in nature or culture to find the constant. First, take a protractor and measure the radius at selected angles. You can do that with the simulation here. Then take the log of each radius, as shown here. Your values will vary depending on the size parameter you use.
| Angle: | 450 | 540 | 630 | 720 |
|---|---|---|---|---|
| Radius: | 24 | 44 | 86 | 163 |
| ln(radius): | 3.17 | 3.78 | 4.45 | 5.09 |
Table of angle versus radius and log
Finally, graph the log of the radius as a function of angle. The slope is .82/270 = .003. So C= 10.003 = 0.5.
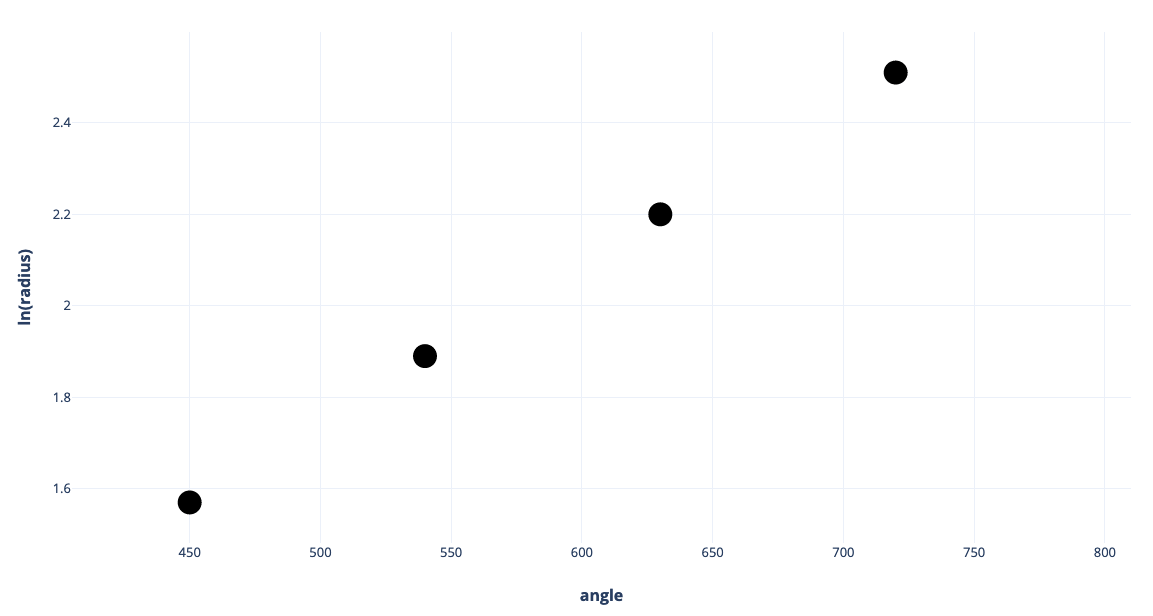
Log of the radius as a function of angle