The Log Spiral Block
How does it work?
Inside the log spiral block in the CSDT Software you can see 5 parameters. Before we dive into the script, let's clarify the parameters:

- C: the “coiled” parmeter. In the language of the adinkra artisans (Twi) they say some spirals are aboapua awan (“tightly coiled”), and others are ntitim awan (“loosely coiled”). We are not imposing western math, we are just translating from their geometric concept to the way it appears in your classroom.
- Sweep: indicates how many degrees the spiral sweeps through.
- Size: how large the overall spiral. Change it to scale as needed
- Pen Growth: how quickly the thickness of the line grows. It can also be negative, shrinking the thickness.
- Clockwise: True/False. Determines whether the final shape is clockwise or not. Note: It doesn't indicate the drawing direction -- that is sweep.
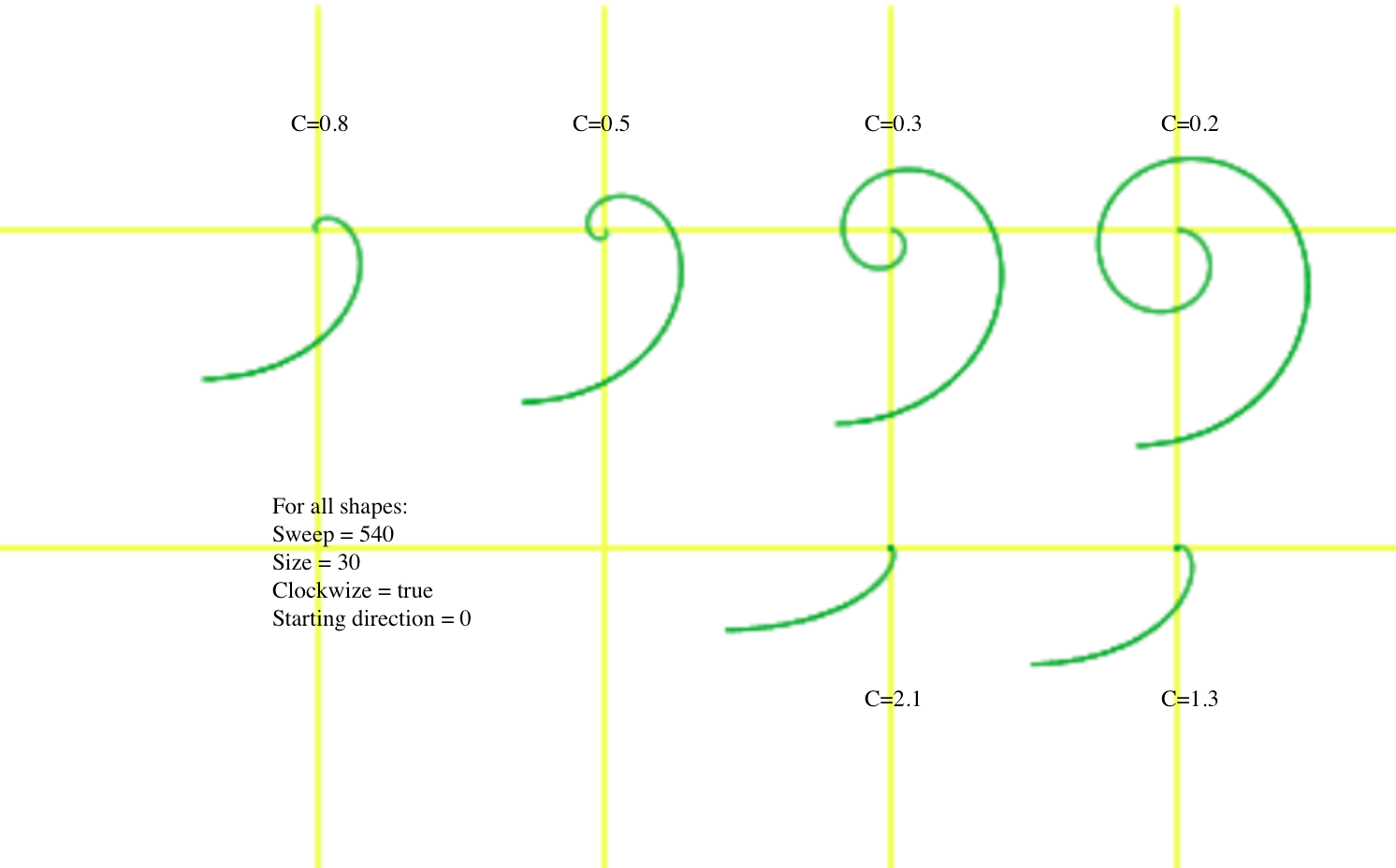
Note that each one sweeps through the same range of angles, it is only the C parameter that changes.
 |
 |
 |
 |
Sweep = 180 |
Sweep = 360 |
Sweep = 720 |
Sweep = 900 |

Sweep = -340 vs -700
Note that if sweep is positive, as in the examples below, we draw from the center, spiraling outward. If the sweep is negative, we start from outside, spiraling inward.
 |
 |
Sweep = -900 |
Sweep = 900 |

As a result, taking out the pengrowth, each unique log-spiral can be identified by their coil(C), sweep (how many degrees they “spiral through”), size, and if they are clockwise/not on the CSDT blocks.
Absolute vs Relative
Frame of Reference
Absolute: If the spiral was some object, like a spiral shell, you could imagine placing that shell anywhere on the stage. In the pen growth examples above, you could see the yellow lines forming grids, such that the center of the shell was exactly at the center of the grid. This absolute coordinate system places the spiral somewhere on the CSDT “stage”-- For example here the gyenayme symbol is at 0.0
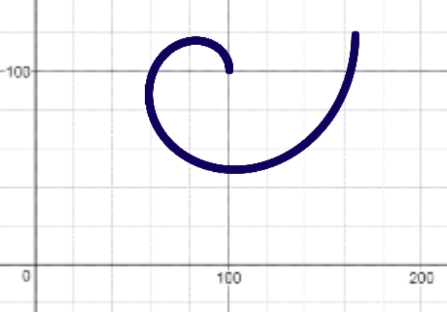
Relative: Going back to the shell analogy, I can have the center of the shell's spiral located anywhere on the stage. So the stage has an absolute center. But the shell has its own center relative to itself. The same for rotation angle. Below is a spiral whose center has an absolute position of 100,100 and absolute rotation of 90. But as I move my mouse along that curve, I could start at the “center” relative to the spiral. That has an absolute angle of 90, but a relative angle of 0.
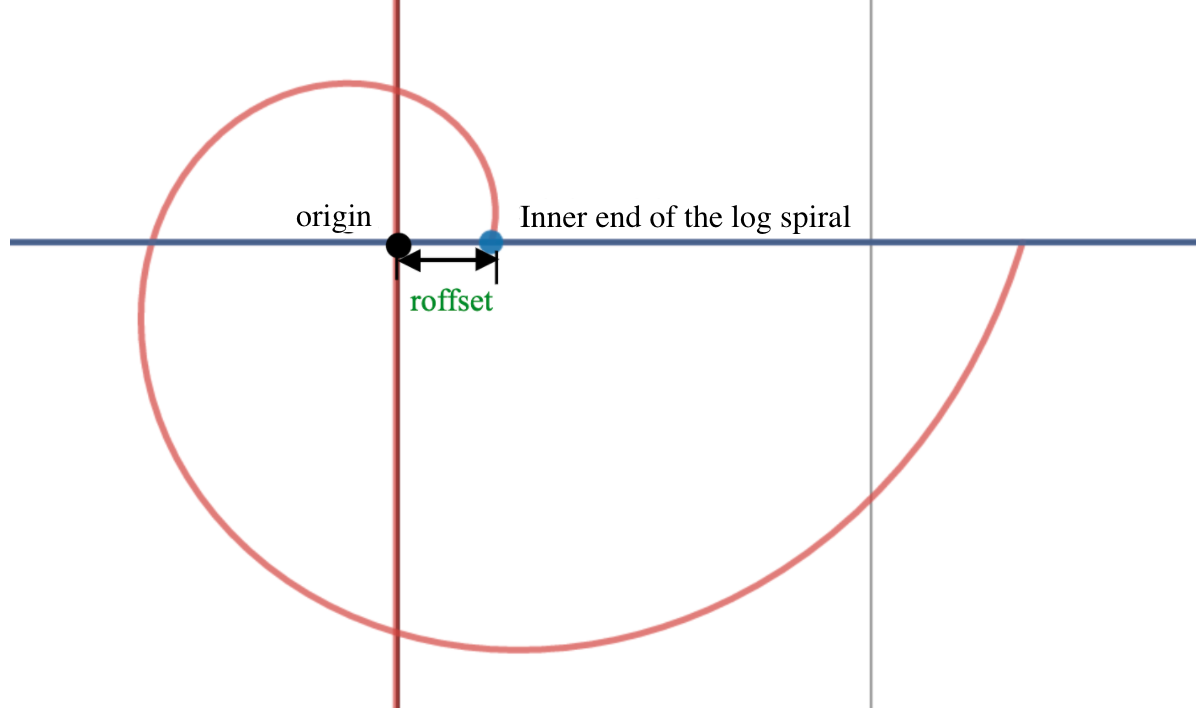
"roffset"
Because we are simulating a continuous curve created by drawing or carving, we do not want to have an unexpected gap between the end of one line and the start of the spiral. So we need to measure the gap and compensate for it. We call this “roffset”, the distance between the center of the spiral and where the spiral ends at the inside.
It is measured by calculating the amount of radius when the angle is zero.
Starting Direction
Besides the radius, we could also draw a tangent line for each point on the spiral, which will always form a consistent, fixed angle with the radius line, as annotated below.
For example if we are drawing from the center to outside, we start at the point with the blue arrow pointing the starting direction.
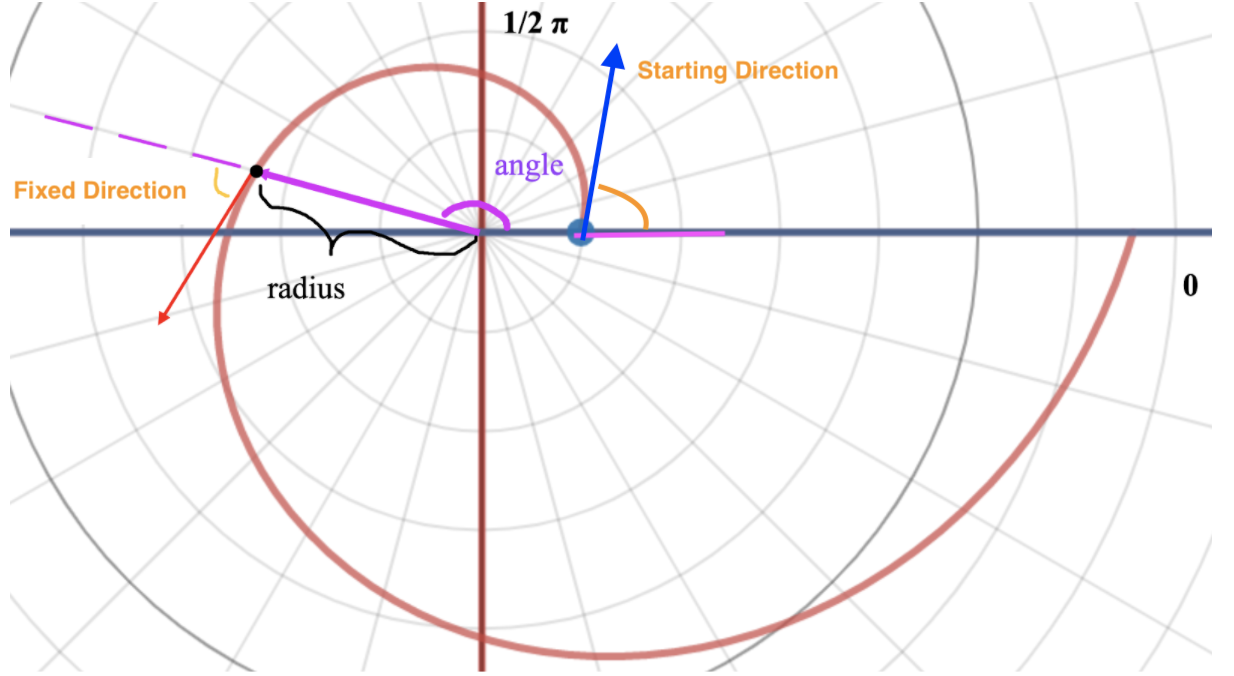
This is one of the properties of a log spiral. → Artisans determine how tightly the spiral coils intuitively. Here, we use C - the “coil” parameter to calculate the Fixed Direction, through the formula below:
arctan(1/C)
Since the angle stays the same in every point of the spiral, including the point which we start drawing from, we will call this a “fixed direction”. When we are at the starting point, we use this to calculate “Starting Direction”, matching the starting direction variable in the script.
Move your mouse on the log spiral blocks, right click “edit”, you could find some scripts that directs the pen collectively: (if it's overwhelming at first to look at, don't worry)
You can find how we calculate the “starting direction” in the blocks below
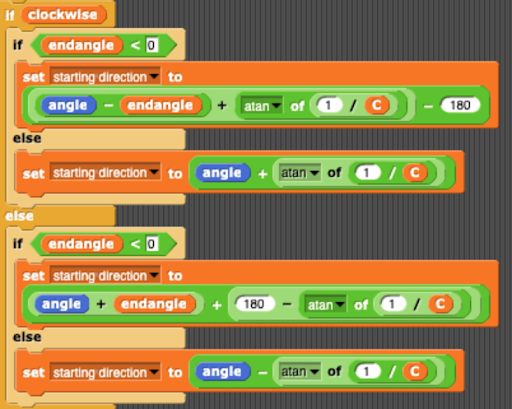
These blocks set the initial starting direction based on user input of the endangle (which has the same value as sweep), and check whether the spiral shape is clockwise or not.
If we enter a c value of zero, we'd result in drawing a circle - because the consistent angle(ψ) would be 90 degrees (½ π)!!
Going back to the stack of blocks that you see behind the log spiral block, this is the block that calculates roffset, which we store in the script variable roffset.

We made use of roffset in the following script which we adjusted the position of the spiral to compensate for this distinction (in blue circle).
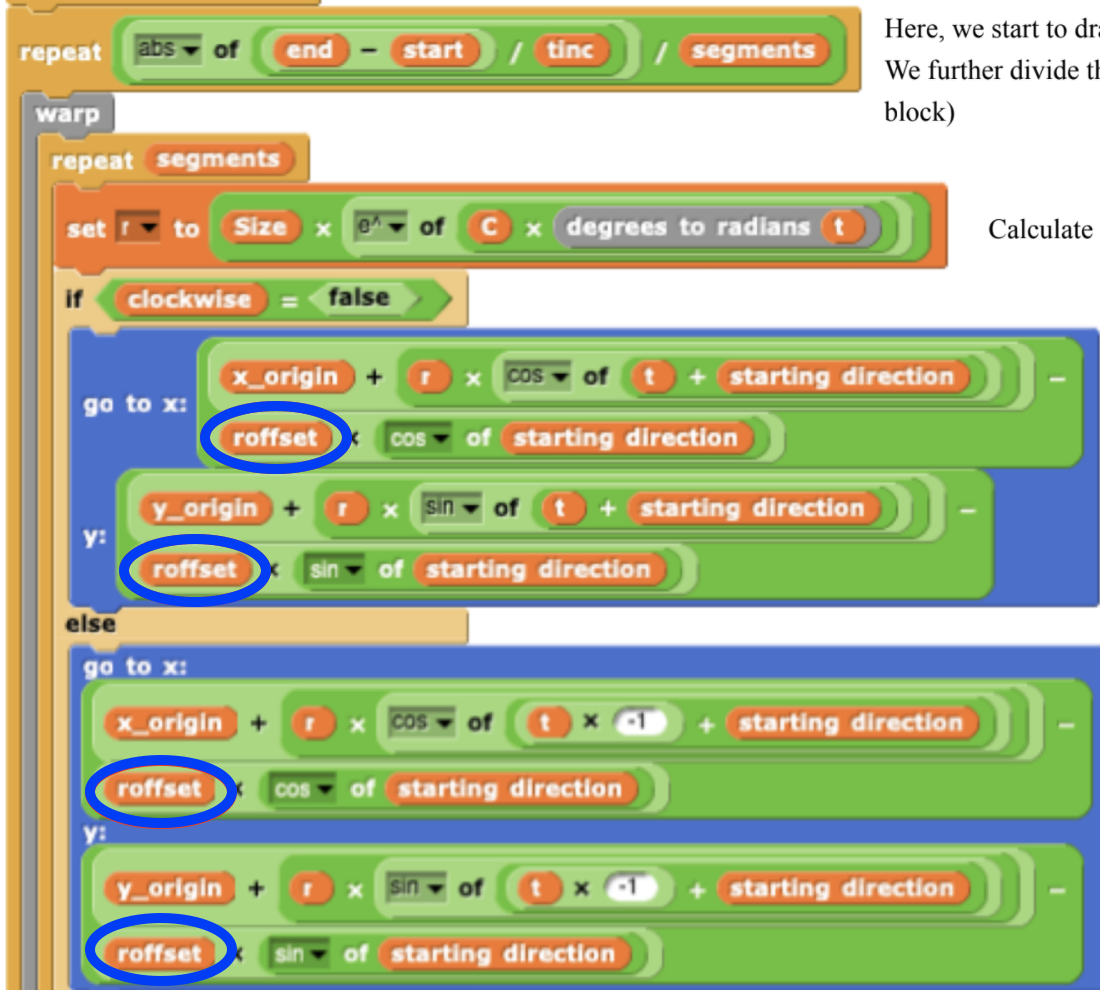
The “segments” are very small increments of straight lines that draw the spiral. So small that the human eye sees them joined as a curve. We draw these little portions one by one with the increase of “tinc”(theta increment). - which we add to the “t” (theta). Theta is the relative angle that we calculate the radius from.

What is relative angle? If we don't consider the rotating of each spiral and consider its starting direction to be angle zero, each point will then just be identified by the radius and its angle. (r, t). [θ - 'theta']
We name it relative angle, because an absolute angle of a point is the value if we put a polar coordinate as the background on the large canvas of CSDT, considering the initial direction of the pen.
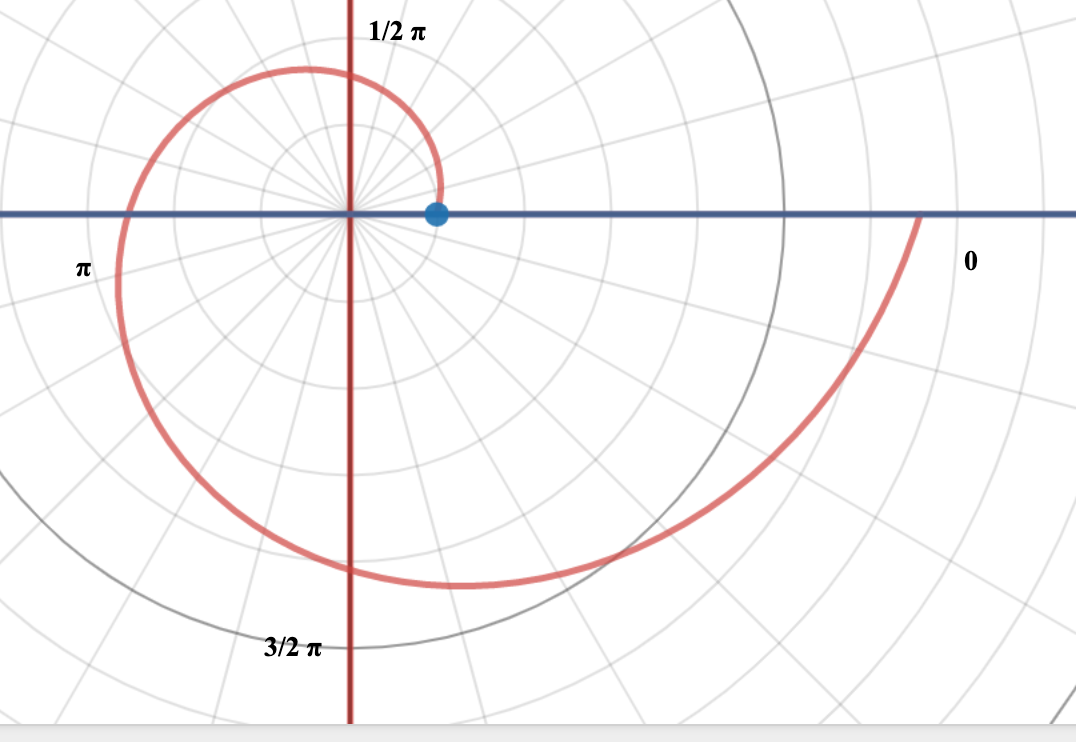
For example, if we are initially pointing straight upward “to the ceiling” (the angle would be 90), keeping the other variables the same with this spiral, we will draw something like this:
Thus, we only need the Relative Angle to calculate radius. In our script, this variable is t.
With each relative angle (marked in purple), we then calculate a radius to find the exact place to put the pen.
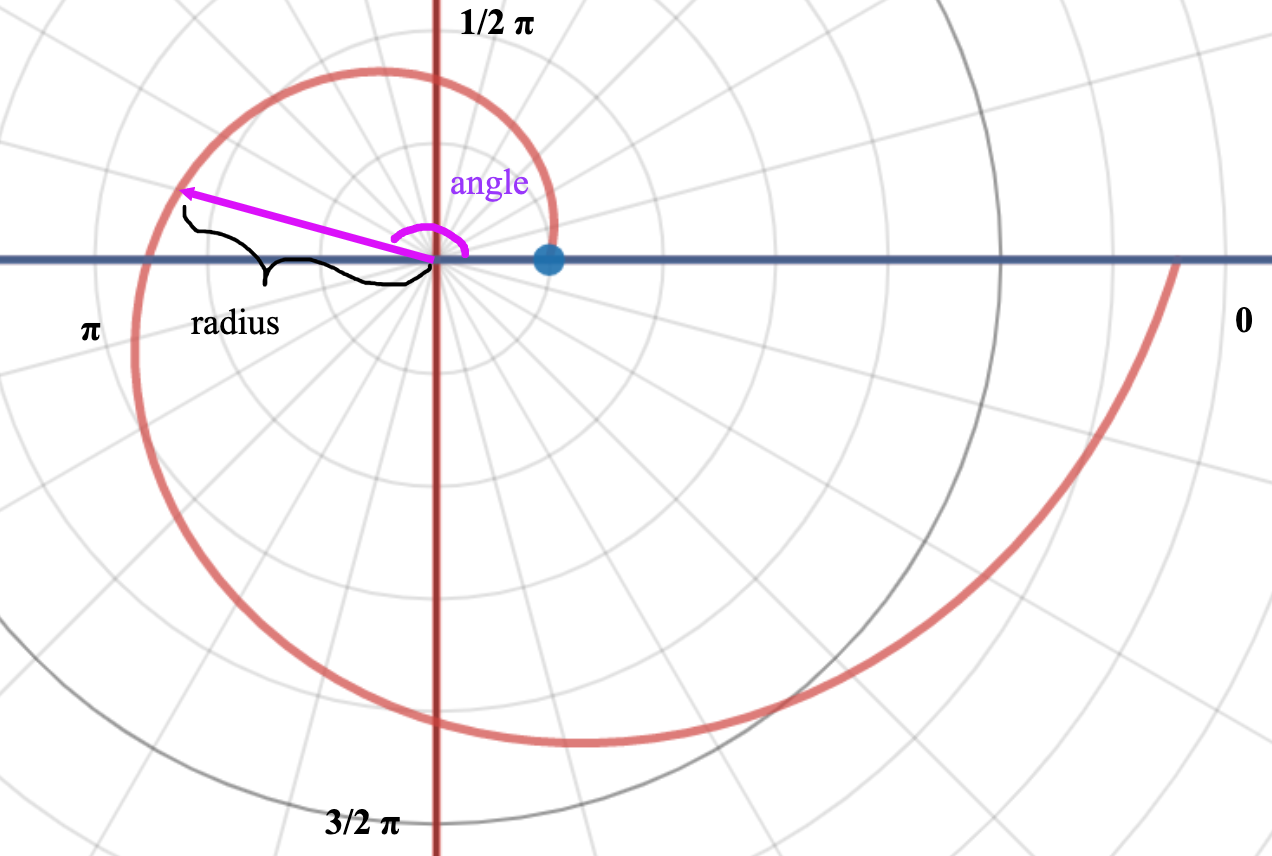
We make use of each step that the angel changes, from which our change for the radius is based on.
Thus the formula that defines every log spiral (notice that c, the coil parameter, is exponentially related to the radius) is:
r= eC*t
We terminate when all the increments are being drawn.


Note: There are differentiations of specific tasks when the input value of sweep is positive or negative, and if the shape is clockwise or not.
To see the full breakdown of the log spiral block, click here.